Biochemistry Online: An Approach Based on Chemical Logic

Biochemistry Online

 CHAPTER 6 - TRANSPORT AND KINETICS 

 
B:  Kinetics of Simple and Enzyme-Catalyzed Reactions

BIOCHEMISTRY - DR. JAKUBOWSKI

4/10/16

Learning Goals/Objectives for Chapter 6B:  After class and this reading, students will be able to

  • write appropriate chemical and differential equations for the rate of disappearance of reactants or appearance of products for 1st order, pseudo first order, second order, reversible first order reactions
  • draw and interpret graphs for integrated rate equations (showing reactant or product concentrations as a function of time) and initial rate equations (showing the initial velocity vo as a function of reactant ;
  • derive kinetic rate constants from data and graphs of integrated rate and initial rate equations;
  • write appropriate chemical, differential equations, and initial rate equations for the rate of disappearance of reactants or appearance of products for simple enzyme catalyzed reaction;
  • differentiate between rapid and steady state assumptions;
  • simplify the initial rate equation containing rate constants for an enzyme catalyzed reactions to one replacing the rate constants with kcat and KM, and give operational and mathematical definitions of those constants;

B2.  Multi-Step Reactions

Reversible First Order Reactions

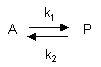
A differential equation can be written for this reaction:

7.   v = d[A]/dt = -k1[A] + k2[P]

This can be solved through integration to give the following equations:

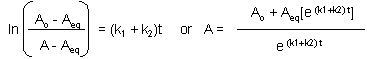
Graphs of A and P vs t for this reaction at two different sets of values of k1 and k2 are shown below.

Figure:  Reversible First Order Reactions:  A <=> P

Xcel Spread Sheet:  Reversible First Order Reactions - 

Go to the following spread sheet and change the values of k1 and k2.  Note the changes in the graphs.  Remember from our discussion of macromolecule:ligand binding, the dissociation constant, Kd, was related to the rate constants by the formula Kd = k2/k1.  Note that if the first order rate constants for a reversible chemical reaction are equal, Keq (and its inverse) equal 1, and the equilibrium concentrations of A and P are equal.

WolframWolfram Mathematica CDF Player - Reversible First Order Reactions ([A] blue, [B] red) (free plugin required)

 

 

SageMathLogoInteractive SageMath Graph:  Reversible 1st Order Reactions

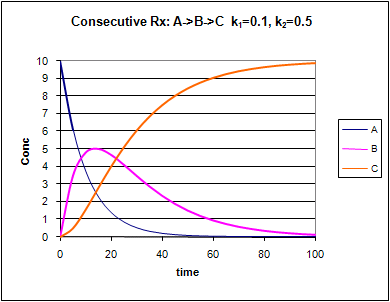
Consecutive First Order Reactions

For these reactions:

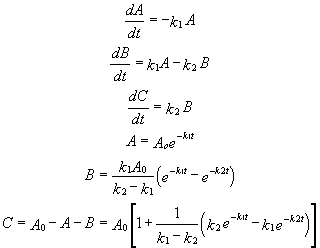
Graphs of A, B, and C vs t for these reaction at two different sets of values of k1 and k2 are shown below.

Figure:  Consecutive Irreversible First Order Reactions:  A --> B --> C

Xcel Spread Sheet:  Consecutive Reactions - 

Change the values of k1 and k2.  Note the changes in the graphs. 

New4/26/13WolframWolfram Mathematica CDF Player - Irreversible Consecutive First Order Reactions ([A] blue, [B] red, [C] orange (free plugin required)

 

 

 

 

SageMathLogoInteractive SageMath Graph: Irreversible Consecutive First Order Reactions

  backNavigation

Return to B:  Kinetics of Simple and Enzyme-Catalyzed Reactions Sections

Return to Biochemistry Online Table of Contents

Archived version of full Chapter 5B:  Kinetics of Simple and Enzyme-Catalyzed Reactions

Creative Commons License
Biochemistry Online by Henry Jakubowski is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.