Biochemistry Online: An Approach Based on Chemical Logic

A
CHAPTER 6 - TRANSPORT AND KINETICS
A: PASSIVE AND FACILITATED DIFFUSION
BIOCHEMISTRY - DR. JAKUBOWSKI
Last Update: 04/08/16
|
Learning Goals/Objectives for Chapter 6A: After class and this reading, students will be able to
|
1. Simple Diffusion
So far we have studied molecular aggregates (micelles and bilayers) and macromolecular structure (mostly proteins). Next we studied binding interactions which are the first steps in the expression of biological activity of a macromolecule. For some proteins, reversible binding is their sole function (consider the binding of dioxygen to myoglobin and hemoglobin). For many others, it is not. For those, what can happen next?
The answer to that question clearly depends on the biological function of the macromolecule. We can simplify this process by adding one additional step as reflected in the equilibrium binding expression shown below:
M + L <==> ML <==> M + X
This expression indicates that the free ligand has changed in some fashion to x. In the next two chapters, we will consider two kinds of transformations:
- L is a ligand on the outside of a
biological membrane (Lout) which binds to a membrane protein receptor,
R. This undergoes a conformational change (as we studied in the binding
of dioxygen to hemoglobin) which leads to the expulsion of the bound
ligand to the inside of the membrane (Lin). This can modeled with the
simple equation:
R + Lout <==> RL <==> R + Lin . This process is called facilitated diffusion and represents a physical as opposed to chemical process since no covalent bonds are made or broken. This process proceeds down a concentration or chemical potential gradient (Δμ < 0) and hence is spontaneous (thermodynamically favored). If the ligand concentration is higher inside the cell, net diffusion moves it to the outside of the cell. Passive (non-facilitated) diffusion is kinetically slow in the absence of a receptor since membranes present formidable barriers to the passage of polar molecules. - L is a ligand (or substrate S) which binds
to a protein enzyme, E. The bound substrate is chemically altered to
produce a new product, P, which dissociates from the enzyme. This can
be expressed most simply as:
E + S <==> ES <==> E + P .
This chapter will discuss diffusion processes. First, diffusion equations will be derived for cases not involving a binding receptor. The equation will show the rate of diffusion of a solute across a membrane from a region of high concentration to a region of low concentration (Δμ < 0) is a linear function of [ΔL] across the membrane. Next we will derive equations for receptor-mediated diffusion across a membrane - facilitated diffusion. We will deal with the situation when the solute must be transported up a concentration gradient (which requires ATP as an exogenous source of energy), a process called active transport, later in this web book.
PASSIVE DIFFUSION THROUGH A MEMBRANE - CASE 1: no receptor

![]() Java
Applet: Before you study the derivation for simple passive diffusion,
view the applet file below. First select clear to remove all
molecules. Add 100 molecules to left. Move speed slider to left just
until in indicates slow. Run the simulation. Count the number
that move to the right hand side in 20 seconds. Refresh browser and repeat
with 200 and then 300 on the left (unfortunately this slows down the
molecules on the left so quantitation is impossible). Graph that
number of molecules that moved to the right chamber (y axis) versus
the the initial number on the left hand side (100, 200, and 300,
respectively, x axis).
Java
Applet: Before you study the derivation for simple passive diffusion,
view the applet file below. First select clear to remove all
molecules. Add 100 molecules to left. Move speed slider to left just
until in indicates slow. Run the simulation. Count the number
that move to the right hand side in 20 seconds. Refresh browser and repeat
with 200 and then 300 on the left (unfortunately this slows down the
molecules on the left so quantitation is impossible). Graph that
number of molecules that moved to the right chamber (y axis) versus
the the initial number on the left hand side (100, 200, and 300,
respectively, x axis).
The flux of molecule A (JA) across a membrane of thickness dx, is proportional to the concentration gradient across the membrane, dA/dx., which is expressed as Fick's First Law of Diffusion:
JA α dA/dx or JA= - D dA/dx
where D is the diffusion coefficient. The negative sign is necessary since concentration increases in the opposite direction of net flux. For these derivations, we will assume the JA is the initial flux. That is, the flux is measured for a short enough time that the relative concentrations of A on both sides of the membrane does not change significantly. It should be clear that eventually the net flux levels off to zero, when the concentrations of A on both sides of the membrane are equal (i.e. the chemical potential of A on both sides is identical).
This can also be expressed as JA = -L dμA/dx , which bridges kinetic and thermodynamic aspects of diffusion.
For JA = - D dA/dx, dimensional analysis shows that
J = moles/area/sec = mol/cm2.s = - (cm2/s) mol/cm3/cm. Hence the units of D are cm2/s.
Rearranging Fick's Law gives the following:
JA = - D dA/dx
�JA dx = -D�dA
Integrate both sides with x varying between 0 and x (the thickness of the membrane), and A from Aout to Ain.
JA x = -D [Ain - Aout] = D [Aout - Ain] or
JA = (D/x) [Aout - Ain] or
JA = P [Aout - Ain]
where P is the permeability coefficient, which has units of cm2/s/cm or cm/s. (We discussed permeability coefficients for different solutes traversing model bilayers when we discussed lipids.)
A plot of JA vs (Aout - Ain) is linear, with a slope of D/x
2. Facilitated Diffusion
Consider the following mechanism:
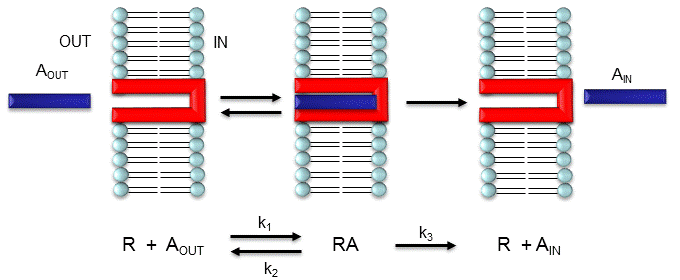
Let's assume that for this system the initial flux will be measured. We would like to derive equations which show J as a function of Aout (assuming that Ain is negligible over the time course of measuring the initial flux. Also assume that the J facilitated is much greater than J passive. In contrast to passive diffusion, JA is not proportional to Aout but rather to [Abound].
Consider this example to help you understand that proportionality. Pretend that the receptor is a truck which can carry one particle across the membrane at a time (i.e. 1/1 stoichiometry). Also assume that the particle can't get across without being carried by the truck. If there are no trucks in the membrane, no load can be delivered. If there are trucks in the membrane but no particles in them, no load will be delivered. As the number of particles available to be loaded into the truck increase, the truck will have an increased chance to be loaded (depending of course on the affinity of the particle for the truck). If the number of loaded trucks is doubled, the number of particles dumped to the other side will double. Therefore, by analogy,
JA is proportional to [RA], or
Equation 1: JA = const [RA] = k3 [RA]
How can we calculate RA when we know A and R? Let us assume that Atotal (A0) is much greater than R0, as is the likely biological case, and Ain = 0. We can calculate RA using the following equations, and the same procedure we used for the derivation of the binding equation
ML = (MoL)/(Kd + L)
Equation 2 - Dissociation constant: K d = ([A]eq[R]eq)/[AR]eq = ([A][R])/[RA] (units of molarity)
Equation 3 - Mass Balance of R: Ro = R + RA so R = Ro -RA
Since we will assume that A0 is much greater than R0, we will not need the mass balance for A (which is Ao = A + RA)
Substitute 3 into 2:
(RA)Kd = (Ro)A - (RRA)A
(RA)Kd + (RA)A = (Ro)A
Equation 4: RA = (Ro)A/(Kd + A)
Substitute 4 into 1 gives the final equation,
Equation 5: JA = const [RA] = k3 [RA] = k3 (Ro)A/(Kd + A).
It should be clear to you from this equations that:
- a plot of JA vs A is hyperbolic
- JA = 0 when A = 0.
- JA = Jmax when A is much greater than Kd
- A = Kd when JA = Jmax/2.
![]() Wolfram
Mathematica CDF Player - Jo vs A (free
plugin required)
Wolfram
Mathematica CDF Player - Jo vs A (free
plugin required)
These are the same conditions we detailed for our understanding of the binding equation
ML = (MoL)/(Kd + L)
RAPID EQUILIBRIUM ASSUMPTION
This derivation is based on the assumption that the relative concentrations of A, R, and AR can be determined by the Kd for the interactions and the concentrations of each species during the early part of diffusion (i.e. under initial rate conditions). Remember under these conditions, Aout does not change much with time. Is this a valid assumption? Examine the mechanism shown in the above figure. Aout binds to R with a second order rate constant k1. RA has two fates. It can dissociate with a first order rate constant k2 to Aout + R (to give the original species), or dissociate with a first order rate constant of k3 to give Ain + R (as A moves across the membrane). If we assume that k2 >> k3 (i.e. that the complex falls apart much more quickly than A is carried in), then the relative ratios of A, R, and RA can be described by Kd. Alternatively, you can think about it this way. If A binds to R, most of A will dissociate, and a small amount will be carried across the membrane. If this happened, then R is now free, and will quickly bind Aout and reequilibrate. This occurs since the most likely fate of bound A is to dissociate, not to be carried across the membrane, since k3 << k2.
Diffusion of Ions and Molecules Across Membranes
As we saw previously, the permeability coefficients of synthetic membranes (liposomes) to solutes is related to the size and polarity of the solute.
Figure: permeability coefficients
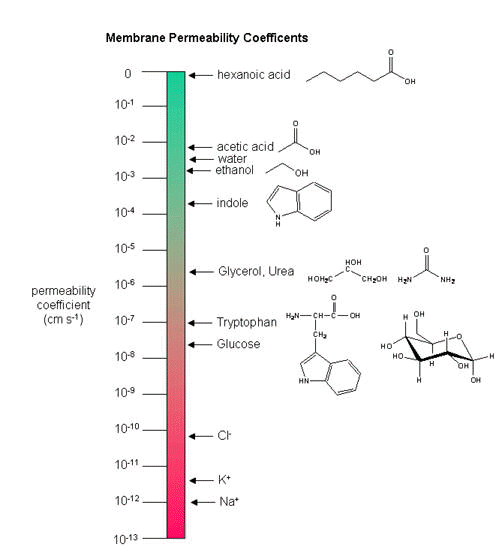
Smaller, higher charge density ions (like Na+) have a lower permeability coefficient than do larger, lower charge density ions (like K+). What about natural membranes? Look at the chart below.
Permeability coefficient (cm/s) of natural and synthetic membranes to D-Glucose and D-mannitol at 25oC.
| Membrane Preparation | D-Glucose | D-Mannitol |
| Synthetic Lipid Bilayer | 2.4 x 10-10 | 4.4 x 10-11 |
| Calculated Passive Diffusion | 4 x 10-9 | 3 x 10-9 |
| Intact Human Erythrocyte (red blood cell) | 2.0 x 10-4 | 5 x 10-9 |
Why do the permeability coefficients differ for D-Glc and D-Mannitol across the red blood cell membrane?
3. "Receptors" in Facilitated Diffusion
Two types of proteins are involved in facilitated diffusion. Carrier proteins (also called permeases or transporters) such as the glucose transporter (GLUT1) move solute molecules across a membrane, Channels facilitate diffusion of ions down a concentration gradient. In the former cases, the ligand binds the receptor (permease, transport protein) which induces a conformational change in the receptor as illustrated in the animation above and in the figure link below.)
Figure: Models for facilitated diffusion of glucose
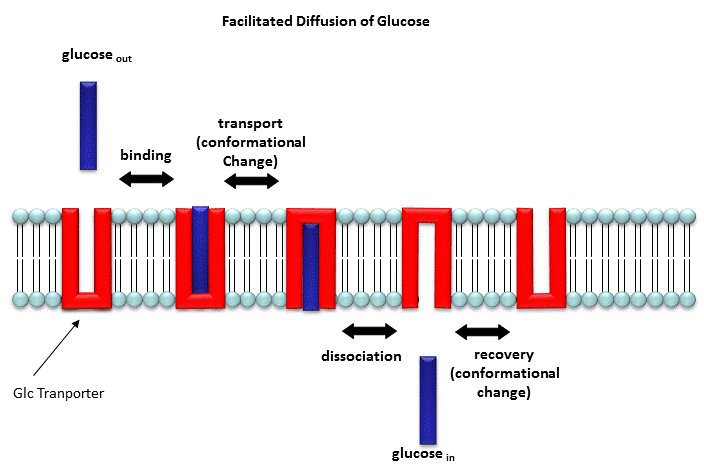
In the latter case, a ligand can bind to the receptor (channel protein) which induces a conformational change in the receptor, a "ligand-gated" channel through the membrane. This process would lead to the diffusion of many ions across the membrane (down a concentration gradient) until the channel closes (which can be induced by ligand dissociation or other events). Clearly, the mathematics we derived for the carrier proteins does not apply to the channel proteins. In addition, there are other ways to "gate" open a channel protein, which we will discuss later. Also some transporters can move solute molecules across a membrane against a concentration gradient. These proteins require an external energy source (like ATP or coupling to the favorable collapse of a second transmembrane gradient ) to drive this thermodynamically unfavored process.
Both links above are from the Theoretical and Computational Biophysics group at the Beckman Institute, University of Illinois at Urbana-Champaign. These molecular dynamic simulations were made with VMD/NAMD/BioCoRE/JMV/other software support developed by the Group with NIH support.
Recently, the x-ray structures of two transporters that are powered by the collapse of a second gradient, were reported.
![]() Jmol:
Updated
Lactose Permease
Jmol14 (Java) |
JSMol (HTML5)
Jmol:
Updated
Lactose Permease
Jmol14 (Java) |
JSMol (HTML5)
![]() Jmol:
Updated Glycerol-3-Phosphate Transporter
From E. Coli
Jmol14 (Java) |
JSMol (HTML5)
Jmol:
Updated Glycerol-3-Phosphate Transporter
From E. Coli
Jmol14 (Java) |
JSMol (HTML5)
Although it is clear that conformational changes in membrane proteins must occur for activity to be expressed, the exact structural rearrangements of these proteins has been difficult to determine given the lack of structural data for membrane proteins, especially as contrasted to water-soluble enzymes. Transporters allow slow (102 to 10-5 s-1) movement of ligands through pores which must be alternately open and closed to allow extracellular and intracellular access/egress. They need at a minimum an "open-to-out" and "open-to-in" conformational states. The pores must be transient and not continuous. Structural studies have been performed on E. Coli Lac Y Permease, a member of the largest transporter family, Major Facilitator Superfamily (MFS). These proteins have two halves with symmetrical halves each with 6 transmembrane domains. Crystal structures suggest a rocker switch like the figure above for the Glu transport protein.
Structural work by Singh et al on the Leu Transporter (LeuT), a member of the solute carrier 6 or sodium coupled transporters, which is an active transporter requiring movement of Na ion into the cells to power the uptake of Leu, show an "open-to-out" and occluded binding state for ligand (Leu). Tryptophan, a competitive nontransportable inhibitors binds to the open-to-out state, but is too large for the obligate occluded state so it is not transported.
Carriers of ligands need not be proteins. Ionophores are small organic molecules which can bind metal ions and move them down a concentration gradient across a bilayer. Most ionophores are not resident in the cell membrane. Rather they are mobile carriers of ions. They bind ions in solution, ferry them through the membrane, and then release them on the other side. As with receptor carrier proteins, they work in both directions but move ions in a net fashion down the concentration gradient of the ion. One example is valinomycin, a natural product of Streptomyces fulvissimus,. It is a cyclic peptide consisting of L and D-Val along with L-lactate and D-hydroxyisovalerate, connected through both ester and amide bonds.
![]()
![]() Jmol:
Valinomycin
Jmol:
Valinomycin
The structure of the valinomycin in its K+ form give clues to its function. The six Val carbonyl oxygens bind the K+ ion. The hydrophilic groups are pointed toward the center, while the hydrophobic groups point to the outside of the structure, allowing the K+ ion to be sequesters in a polar environment as the nonpolar exterior of the complex passes through the membrane. This ionophore is specific for K+ and binds the smaller Na+ ion weakly. This can be accounted for by two factors. The smaller sodium ion doesn't bind as tightly to the chelating carbonyl oxygens. Also, the sodium ion has a higher charge density, so the Na+/water interactions must be more stable and more difficult to break than those to K+. The ion must be desolvated before it binds to the complex. Other ionophores are specific for other ions.
Some ionophores, like gramicidin, from Bacillus brevis, forms a pore in the membrane through which different types of Group I ions may flow. It is a 15-residue peptide consisting of alternating D and L amino acids of significant hydrophobicity. The peptide appears to form a dimer helix (not an alpha helix, however), in a bilayer membrane.
![]()
![]() Jmol
: Gramicidin
Jmol
: Gramicidin
(go to the bottom link for next page in the top frame of this page and continue until you get to the Gramicidin page - an incredible Chime presentation.)
Aquaporins are tetrameric complexes that facilitate water diffusion through bilayers. They have amazing selectivity as they don't pass other solute or even protons (H3O+ or naked H+ ions). See the amazing link below to molecular dynamics simulations of the process.
![]()
![]() Jmol: Aquaporin
Jmol: Aquaporin
![]() Jmol: Updated
Aquaporin Monomer
Jmol14 (Java) |
JSMol (HTML5)
Jmol: Updated
Aquaporin Monomer
Jmol14 (Java) |
JSMol (HTML5)
Gram negative bacteria (as well as mitochondria in eukaryotic cells) have protein complexes called porins (different from the aquaporin discussed above). The monomer porin forms a trimer in the membrane which forms a pore allowing small solute molecules necessary for bacterial cell growth to pass. The porin proteins share a 16 stranded anti-parallel beta barrel as a common motif. Solute molecules can pass through the pore created by the beta barrel. An example, maltoporin, is shown below:
![]() Jmol: Updated
Maltoporin Transport Protein
Jmol14 (Java) |
JSMol (HTML5)
Jmol: Updated
Maltoporin Transport Protein
Jmol14 (Java) |
JSMol (HTML5)
4. Membrane Pores
The Nuclear Pore Complex
Channels have pores which can be gated open and allow selective flow of ions. Porins have larger entrances which allow larger molecules to pass the bilayer. The biggest pore structure known is the nuclear pore complex, which has a combined molecular mass around 125,000,000! It's job is to shuttle small molecules through passive diffusion down a concentration gradient through the pore. In addition it moves large molecules and molecular structures (proteins, RNA, and perhaps ribosomes) across the nuclear membrane in a process which requires energy. The proteins that comprise this complex are called nucleoporins, of which there appears to be around 30 in yeast. Large proteins that pass through the pore must first be bound to a cargo receptor, which can move the "cargo" across the pore with concomitant GTP hydrolysis.
Figure: Movement of Molecules and Particles Through Membranes
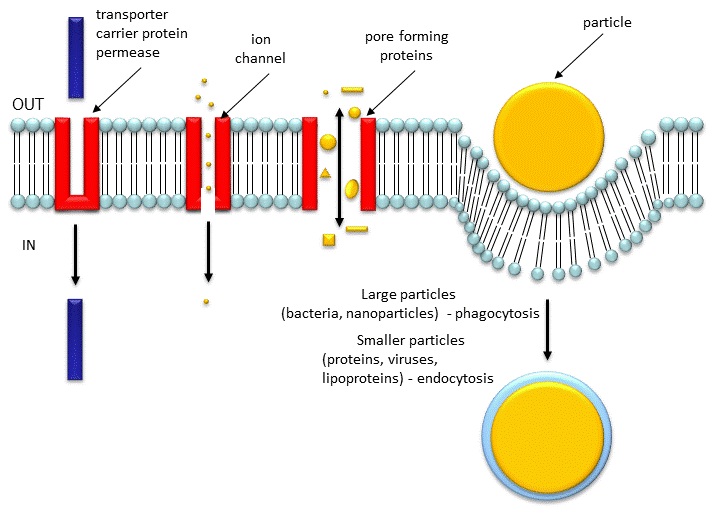
Porins: TBA
5. Cell Junctions - TBA
Drugs and Diffusion
One of the biggest challenges in medical drug development is the synthesis of drugs that can diffuse across the cell membrane. This requires that the drug be sufficiently nonpolar while at the same time it must be sufficiently polar to have reasonable aqueous solubility, allowing blood transport. One way around this problem is to develop a water soluble drug and a protein "receptor" which would allow drug passage across the membrane. A novel mechanism not based on facilitated diffusion has been developed that allows certain protein sequences to transduce the drug across the membrane (a process called protein transduction or molecular transportation). Researchers have looked to nature to find proteins which can move across the membrane and adapted them for this process. Several viral proteins (including TAT from the HIV virus) possess such properties, which require the presence of a short "transporter" amino acid sequence in the protein. Drugs are covalently attached to the sequence, and carried through the membrane by the short protein sequence. This mechanism does not fit the criteria of facilitated diffusion since the required protein fragment is not a classical receptor. It is amphiphilic and can pass through the membrane even if synthesized in the lab using D-amino acids or if the sequence is scrambled. The fusion domain of the TAT protein is ionic (containing 5-15 Arg residues) and probably interacts initially with negatively charged glycosoaminoglycans on the cell surface. Many different types of drugs can be delivered in this fashion (large to small, proteins, nucleic acids, and large liposomes, etc).
Another approach is to design artificial receptors. For example, a ligand that might ordinarily bind to a protein could be covalently modified with a hydrophobic group (often a cholesterol derivative) which would allow it to partition into the cell membrane, exposing the ligand on the cell surface. The surface ligand can then bind its target protein. If the protein is multivalent (can bind more than one ligand per protein, such as an antibody), lateral diffusion and clustering of protein-artificial receptor complexes in the membrane can occur, as well as the formation of lipid rafts. Similar to other ligand-receptor interactions that display such properties, these membrane changes can lead to endocytosis of the protein-artificial ligand complex.
6. Links and References
- Science 322: 1655 (2008)
- Huang, Y. et al. Structure and mechanism of the Glycerol-3-Phosphate Transporter from E. Coli. Scinec. 301, pg 616-620 (2003)
- Abramson, J. et al. Structure and mechanism of the Lactose Permase of E. Coli. Science. 301, pg 610-615 (2003)
- Locher, K. et al. Breaching the Barrier (review of transport proteins LacY and GlpT. Science. 301, pg 603 (2003)
- Alper, J. Breaching the membrane (new ways to move drugs through membranes). Science. 296. pg 838 (2002)
- Murata et al. Structural Determinants of Water Permeation through Aquaporin I. Nature. 407, pg 599 (2000)
- Fu et. al. Structure of a glycerol-conducting channel and the basis for its selectivity. Science 290. pg 481 (2000)
- Sui et al. Structural basis of water-specific transport through the AQP1 water channel. Nature. 414. pg 872 (2001)
- deGroot and Grubmuller. Water Permeation Across Biological Membranes: Mechanism and Dynamics of Aquaporin-1 and GlpF. Science. 294. pg 2304, 2353 (2001)
- Aqivst and Luzhkov. Ion permeation mechanism of the potassium channel. (dynamics results). Nature. 404 pg 881 (2000)

Biochemistry Online by Henry Jakubowski is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.