CHAPTER 9 - SIGNAL TRANSDUCTION

F:  Signaling Math - Graphical Analyses of Inputs and Outputs  

Wilmot Osei-Bonsu and Henry Jakubowski

11/16/17 New and slowly evolving ....

F1. Single Time Inputs

A.  Simple Enzyme:  Product vs time

First let's review a simple example of an enzyme (E), that binds a single substate (S) to form a single product. 

We have derived equations for this mechanisms for both the rapid equilibrium (when k₃<<k₂) and the steady state conditions.  Let's consider the more general case of the steady state.  In a way the equation could be modeled as shown below but with out the inhibitory steps of inhibitor (I) or product (P) binding to the enzyme, which is represented as a node (open square) in the diagram.

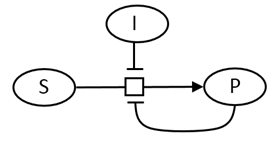
To derive the steady state equation, we made the assumption that shortly after addition of the input signal (substrate at a fixed concentration), the [ES], at least in the early part of the reaction where initial rate conditions prevail, is constant.  Hence the following two equations hold:

v = k₃[ES]  and in the steady state,  d[ES]/dt = k₁[E][S] - k₂[ES] -k₃[ES]= 0

It is easy to write the differential equations for the other three mass action species:

d[E]/dt = k₂[ES] + k₃[ES];  d[S]/dt = k₁[E][S];  and d[P]/dt = k₃[ES]                

These 4 sets of ordinary differential equations can be numerically solved.  The concentrations of each species as a function of time are shown below.  Pay close attended to [ES] vs time which levels off a short time into the reaction, showing the validity of the steady state assumption.  Likewise note [P] vs time, which represents the simple "output" in this model system.

11/16/17Wolfram Mathematica CDF Player - Initial Input of Substrate to an enzyme:  Output vs Time (free plugin required)

A  downloadable version for use with the free, standalone CDF player (no browser required)

B.  Simple Enzyme - Product vs time: Competitive Inhibition by product.

Now, let's start adding additional interactions, in this case feedback product inhibition.  Previously we derived and displayed static and interactive graphs for competitive inhibition, which show initial velocity as a function of varying substrate concentration at different fixed concentrations of inhibitor.  Now lets looks at graphs of output ([P]) plus and minus inhibitor, as a function of time.  The chemical equations and modern symbolic notion for it is shown below.

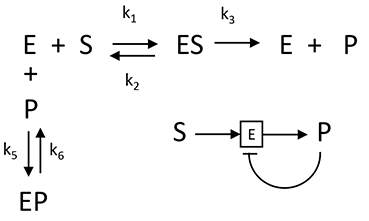
The following ordinary differential equations can be written for interactions:

Wolfram Mathematica CDF Player - Output vs Time:  Product inhibition (free plugin required)

A  downloadable version (not yet available - working on it!) for use with the free, standalone CDF player (no browser required)

C.  Simple Enzyme - Product vs time: Feedback Inhibition by Product of Two Enzyme System.

Now consider inhibition of the first enzyme in a pathway by the final product of the pathway.  For mathematical simplicity our system will consist of two linked enzymes.  You should expect that the inhibition curve as a function of time would be similar to simple product inhibition in a one-enzyme system.  The chemical and mathematical equation describing the interactions of substrates, products and enzymes are shown below.

Chemical Equations for Product Inhibition in a "Two-Enzyme" Pathway

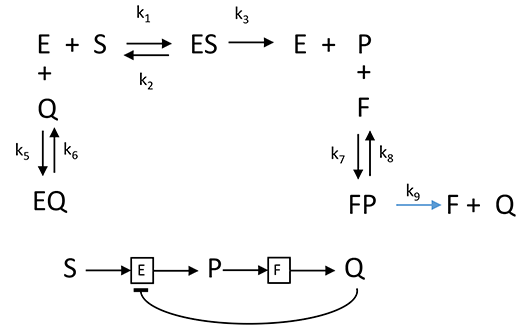
Mathmatical Equations for Product Inhibition in a "Two-Enzyme" Pathway

Wolfram Mathematica CDF Player - Output vs Time:  Product inhibition (free plugin required)

A  downloadable version (not yet available - working on it!) for use with the free, standalone CDF player (no browser required)

D.  Product vs time: Two Enzyme System with feedback inhibition and activation.

Of course, metabolic and signal transductions pathways must have both inhibition and activation signals if pathways are to respond to the plethora of biological needs.  Since the mathematical complexity of the output scales with the number of interacting participants, lets simplify the analysis by considering two linked enyzes, E and F, in which the product of the final enzyme F feedback inhibits the first enzyme E while the product P of the first reaction of E binds back to the enzyme (at perhaps an allosteric site to form a modified version of the G) and activates the first enzyme.  This leads to an oscillatory output of the final product of the pathway, Q, vs time.

Chemical Equations for Feedback Inhibition and Activation for a Two-Enzyme" Pathway

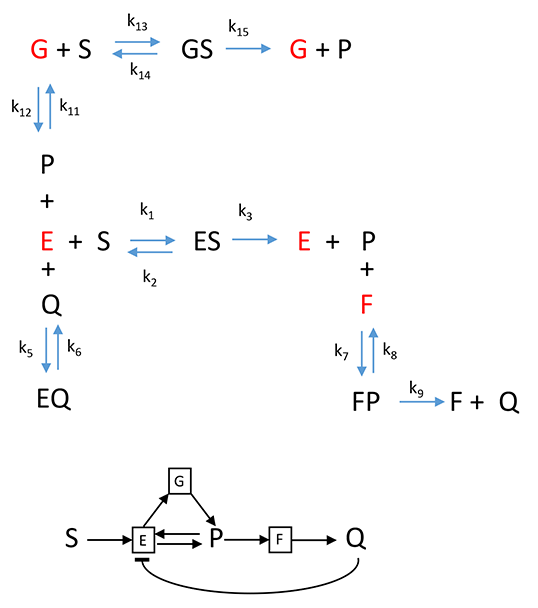
adfdfferee

Mathematical Equations for Feedback Inhibition and Activation for a  "Two-Enzyme" Pathway

Wolfram Mathematica CDF Player - Output vs Time:  Feedback inhibition AND activation (free plugin required)

A  downloadable version (not yet available - working on it!) for use with the free, standalone CDF player (no browser required)

Navigation

Return to Chapter 9F:  Signaling Math - Graphical Analyses of Inputs and Outputs

Return to Biochemistry Online Table of Contents